Spot Size Converter
Introduction
The function of Spot Size Converter (SSC) is to connect silicon photonics integrated chips and external optical fibers, which can couple light transmitted in silicon waveguides into the fiber at low loss. As shown in the figure, SSC has a tapered silicon waveguide with gradually thinning ends and a low refractive index waveguide covered with SiON, and the entire waveguide device is placed in a silicon dioxide environment [1]. The mode field size at the end of the tapered waveguide is similar to that of the optical fiber, so it can effectively couple light from the waveguide into the fiber.
Eigenmode expansion (EME) method has great advantages in designing long taper waveguide. Because using length scanning in analysis does not calculate any modes, only the bidirectional transmission part is calculated. The calculation of modes is achieved by dividing the structure with cross-sectional changes in transmission direction into multiple cells, and using FDE solver to calculate at the interface between adjacent cells.
Simulation
1. Code Description
1.1 Import Toolkit
First, we need to import "maxoptics_sdk" and third-party package of Python. The import module of EME simulation as follows.
import maxoptics_sdk.all as mo
from maxoptics_sdk.helper import timed, with_path
import os
import time
from typing import NamedTuple
1.2 Define Simulation Function
def simulation(*, wavelength=1.55, grid=0.08, number_of_modes=10, run_options: "RunOptions", **kwargs):
wavelength: controls the wavelength to be solved.
grid: controls the mesh size of the simulation region.
number_of_modes: controls the number of modes to be calculated.
1.3 Define Parameters
Before starting the simulation, we can define parameters to facilitate modeling and parameterization sweep. The defined parameters as follows.
# region --- 0. General Parameters ---
path = kwargs["path"]
simu_name = "EME_SSC"
time_str = time.strftime("%Y%m%d_%H%M%S", time.localtime())
project_name = f'{simu_name}_{run_mode}_{time_str}'
plot_path = f'{path}/plots/{project_name}/'
gds_file_root_path = os.path.abspath(os.path.join(path, '..'))
gds_file = gds_file_root_path + "/examples_gds/SSC.gds"
# endregion
path: this parameter is used to the absolute path of this Python file.
plot_path: this parameter is the path where the calculation results are saved.
time_str: this parameter is used to store the timestamp.
gds_file: this parameter is used to store the file path of GDS.
1.4 Create project
We create an empty project by instantiating "Project()" in the simulation environment and define the name of project.
# region --- 1. Project ---
pj = mo.Project(name=project_name)
# endregion
1.5 Add Material
After using "Material()" to instance the material module into the project, "add_nondispersion" and "add_lib" functions are available to create materials. You can refer to the following script to set materials.
# region --- 2. Material ---
mt = pj.Material()
mt.add_nondispersion(name="Si", data=[(3.476, 0)], order=2, color="#BF2C2C")
mt.add_nondispersion(name="SiO2", data=[(1.465, 0)], order=2, color="#D4E5FE")
mt.add_nondispersion(name="SiON", data=[(1.50, 0)], order=2, color="#FBBBBB")
mt.add_lib(name="Air", data=mo.Material.Air, order=2)
# endregion
The "name" defines the name of the added material.
The "data" specifies the real and imaginary parts of the refractive index of the material.
The "order" specifies the mesh order of the material.
1.6 Add Structure
The structure is composed of silicon dioxide substrate, adiabatic tapered silicon waveguide and polymer covered waveguide. We use "Structure()" to instance the structure module to the project, "add_geometry" function is available for adding structures. By selecting the type of gds_file, you can establish structure by importing the gds file method.
# region --- 3. Structure ---
st = pj.Structure()
st.add_geometry(name="sub", type="gds_file",
property={"general": {"path": gds_file, "cell_name": "SSC", "layer_name": (1, 0)},
"geometry": {"x": 0, "y": 0, "z": -1.5, "z_span": 3},
"material": {"material": mt["SiO2"], "mesh_order": 1}})
st.add_geometry(name="ssc", type="gds_file",
property={"general": {"path": gds_file, "cell_name": "SSC", "layer_name": (2, 0)},
"geometry": {"x": 0, "y": 0, "z": 0.1, "z_span": 0.2},
"material": {"material": mt["Si"], "mesh_order": 2}})
st.add_geometry(name="cover", type="gds_file",
property={"general": {"path": gds_file, "cell_name": "SSC", "layer_name": (3, 0)},
"geometry": {"x": 0, "y": 0, "z": 1.5, "z_span": 3},
"material": {"material": mt["SiON"], "mesh_order": 1}})
# endregion
The properties of GDS modeling are shown in the table below.
| Key | Value | Type | Description |
|---|---|---|---|
| path | gds_file | string | The file path of GDS file |
| cell_name | SSC | string | The cell name of the GDS. |
| layer_name | (1,0) | list | The name of the GDS layer |
| x | 0 | float | The center position in the x-direction of the geometry |
| y | 0 | float | The center position in the y-direction of the geometry |
| z | -1.5 | float | The center position in the z-direction of the geometry |
| z_span | 3 | float | The length of the geometric structure in the z-direction |
| material | mt["Si"] | material | Selects a material from material database |
| mesh_order | 2 | integer | Selects a material in overlapping region when generating grids, the material with higher mesh order have higher priority. |
1.7 Add Simulation
We use the "Simulation()" to instance the simulation module into the project and the "add" function to add an EME solver for the simulation.
According to different geometric structures and materials, the SSC is divided into four cell groups using "cell_group_definition". Set the length of the cell group in "span", use "cell_number" to set the number of cell. The divided cell structure is shown in the following figure. Use "number_of_modes" to set the number of modes calculated at the interface of adjacent cells, and it is necessary to set a sufficient number of modes to obtain the correct results.
The region where the cross-section of structure has not changed, the number of "cell_number" set to 1, and "sc" set to "none". In the region of structural changes, multiple cell number need to be used to characterize the structure and the "sub_cell" method is used to reduce the staircase effect caused by discrete changes of the cross-section.
# region --- 4. Simulation ---
simu = pj.Simulation()
simu.add(name=simu_name, type="EME",
property={"general": {"wavelength": wavelength, "use_wavelength_sweep": True},
"background_material": mt["SiO2"],
"mesh_settings": {"mesh_factor": 1.2, "mesh_refinement": {"mesh_refinement": "curve_mesh"}},
"geometry": {"x_min": -103, "y": 0, "y_span": 5.5, "z": 0.5, "z_span": 7},
"boundary_conditions": {"y_min_bc": "PEC", "y_max_bc": "PEC", "z_min_bc": "PEC", "z_max_bc": "PEC"},
"eme_setup": {"cell_geometry": {"allow_custom_eigensolver_settings": True,
"cell_group_definition": [
{"span": 2, "cell_number": 1, "number_of_modes": number_of_modes, "sc": "none"},
{"span": 1, "cell_number": 1, "number_of_modes": number_of_modes, "sc": "none"},
{"span": 200, "cell_number": 30, "number_of_modes": number_of_modes, "sc": "sub_cell"},
{"span": 3, "cell_number": 1, "number_of_modes": number_of_modes, "sc": "none"}]}},
"transverse_mesh_setting": {"global_mesh_uniform_grid": {"dy": grid, "dz": grid}}
})
# endregion
The properties of the EME solver are shown in the table below.
| key | value | type | description |
|---|---|---|---|
| wavelength | 1.5 | float | wavelength of mode |
| use_wavelength_sweep | True | bool | select to enable wavelength sweep |
| eme _propagate | True | bool | select to enable EME propagation |
| propagation_sweep | True | bool | select to enable length sweep |
| span | 2 | float | the span of cell group |
| cell_number | 1 | float | number of cell in the cell group |
| number_of_modes | 15 | float | Calculate the number of modes per cell |
| sc | none | string | select to enable subcell method |
| dy | 0.05 | float | horizontal mesh of cross-section |
| dz | 0.05 | float | Longitudinal mesh of cross-section |
| number_of_points | 50 | float | number of sweep lengths |
1.8 Add EME port
We use the "Port()" to instance the port object into the project and the "add" function to add EME ports for the simulation. At least two ports need to be added for EME simulation to serve as excitation sources and monitors.
# region --- 5. Port ---
pjp = pj.Port()
pjp.add(name="left_port", type="eme_port",
property={"geometry": {"port_location": "left"},
"eme_port": {"general": {"mode_selection": "fundamental_TE", "number_of_trial_modes": number_of_modes}},
})
pjp.add(name="right_port", type="eme_port",
property={"geometry": {"port_location": "right"},
"eme_port": {"general": {"mode_selection": "fundamental_TE", "number_of_trial_modes": number_of_modes}},
})
# endregion
The properties setttings of the EME port are shown in the table below.
| Key | Value | Type | Description |
|---|---|---|---|
| port_location | left | string | selects the location of the port |
| y | 0 | float | The center position of port |
| y_span | 5.5 | float | port width |
| y | 0.5 | float | center position of port height |
| z_span | 7 | float | port height |
| mode_selection | fundamental_TE | string | select the mode of port |
| number_of_trial_modes | 15 | integer | set the number of port modes |
1.10 Add Local Mesh
After light passes through tapered silicon waveguide that gradually becoming smaller, the mode field is strongly limited to a very small range. Therefore, it is necessary to use "LocalMesh" to add fine transverse grids to accurately calculate the limited light field. Adding local mesh as shown below.
# region --- 5. Sub Mesh ---
lm = pj.LocalMesh()
lm.add(name="sub_mesh",property={"general": {"dx": grid, "dy": grid, "dz": grid},
"geometry": {"x": 0, "x_span": 206, "y": 0, "y_span": 5.5, "z": 0.5, "z_span": 7}})
# endregion
The dx/dy/dz are the mesh sizes in the x, y, and z directions, respectively. Note that in the EME simulation, only the grid settings for dy and dz are valid.
1.12 Show Structure
You can use the "structure_show" function to view the top view of the structure, or use the "show3d()" call gui to check simulation settings.
# region --- 9. Structure Show ---
st.structure_show(fig_type="png", show=False, savepath=plot_path + simu_name, simulation_name=simu_name, celldisplay=True, xyratio=(1, 40))
#simu[simu_name].show3d()
# endregion
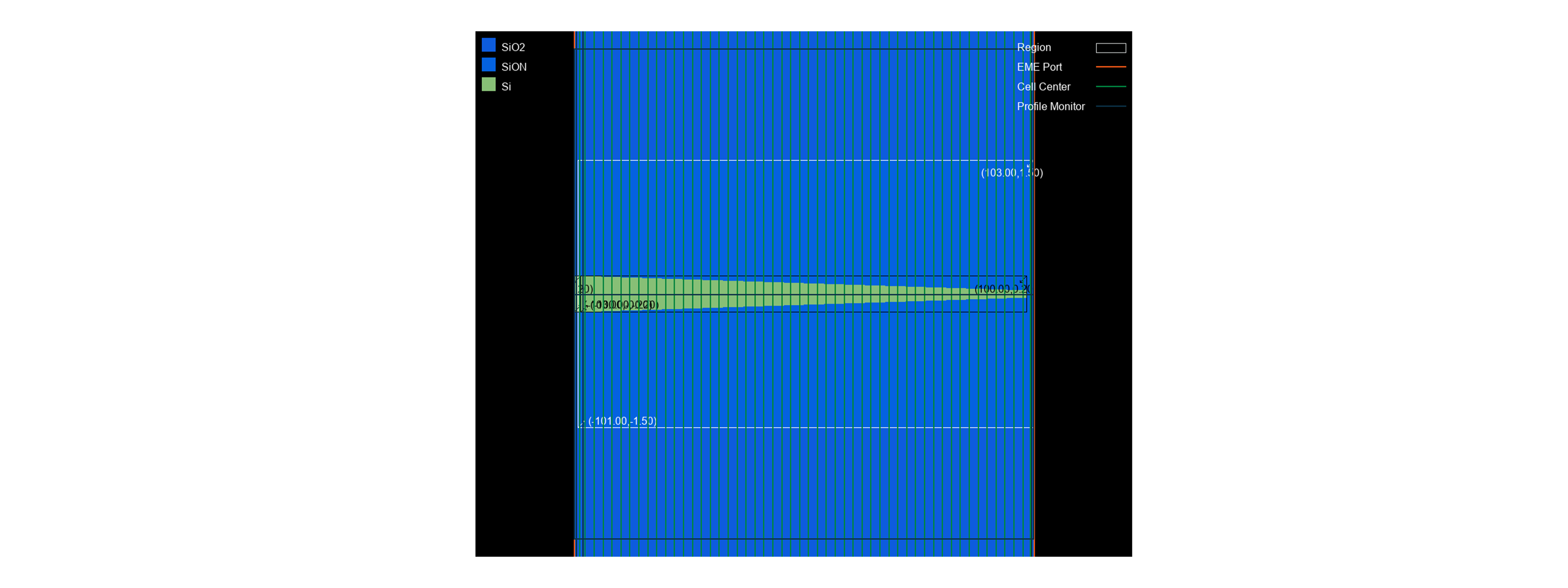
The "celldisplay" control whether to display the boundaries of the divided cells.
The "xyration" controls the aspect ratio of the image.
1.13 Preview Modes
Before running EME simulation calculations, we can calculate the mode field distribution of the port by setting the type of mode selection to True and other simulations to False.
# region --- 10. Calculate Mode ---
if run_options.calculate_modes:
for port in ["left_port", "right_port"]:
simu[simu_name].preview_modes(port_name=port, savepath=f"{plot_path}_modeprofile_{port}",
target="intensity", attribute="E", mode=0, real=True, imag=True, show=False, export_csv=True)
# endregion
1.14 Run and Analysis
When conducting post-processing analysis for EME, it is necessary to first run the solver to obtain the calculation mode results for each unit. The example of the script is shown below.
# region --- 11. Run ---
eme_base_res = simu[simu_name].run()
analysis = pj.Analysis()
analysis.add(name="eme_propagate", type="eme_analysis",
property={"workflow_id": eme_base_res.workflow_id, "eme_propagate": run_options.run,
"energy_conservation":"make_passive",
"periodicity": {"periodicity": False},
"group_span_sweep": {"group_span_sweep": run_options.run_length_sweep, "parameter": "group_span_1", "start": 50, "stop": 250, "number_of_points": 5},
"wavelength_sweep": {"wavelength_sweep": run_options.run_wavelength_sweep, "start": 1.5, "stop": 1.6, "number_of_wavelength_points": 11},
# "override_wavelength":{ "wavelength": 1.55 }
})
eme_res = analysis["eme_propagate"].run()
# endregion
1.15 Extract Results
The extract function is used to extract data from the result data. The script demonstration is as follows.
# region --- 12. see result ---
eme_res.extract(data="eme_propagate:facet_data", savepath=plot_path, real=True, imag=True, export_csv=True)
eme_res.extract(data="eme_propagate:smatrix", savepath=plot_path + "011_eme_smatrix_intensity",
target="intensity", export_csv=True)
eme_res.extract(
data="eme_propagate:monitor", savepath=plot_path + "013_eme_y_normal",
monitor_name="y_normal", attribute="E", export_csv=True)
eme_res.extract(data="eme_propagate:monitor", savepath=plot_path + "014_eme_z_normal",
monitor_name="z_normal", attribute="E", export_csv=True)
for i in range(3):
eme_res.extract(data="eme_propagate:monitor", savepath=plot_path + "0"+str(15+i)+"_eme_section"+str(i+1),
monitor_name="section"+str(i+1), attribute="E", export_csv=True)
# --- EME Propagation Sweep Results ---
if run_options.run_length_sweep:
eme_res.extract(data="propagation_sweep:sweep", savepath=plot_path + "10_length_sweep", export_csv=True)
# endregion
The "eme_propagate:facet_data" stores the calculation mode of cells and ports and the total S-matrix.
The "eme_propagate:smatrix" stores the S-matrix after bidirectional transmission of the calculation port mode.
The "propagation_sweep:sweep" stores the S-matrix corresponding to each length after sweeping.
1.16 Control Switch
We can control the operation of the simulation by passing in bool values through tuple, as shown in the following code.
class RunOptions(NamedTuple):
calculate_modes: bool
run: bool
run_length_sweep: bool
extract: bool
if __name__ == "__main__":
simulation(run_mode="local", wavelength=1.5, grid=0.02, number_of_modes=20,
run_options=RunOptions(calculate_modes=True, run=True, run_length_sweep=True, extract=True))
2 Output Results
2.1 ModeProfile
We extracted the first two modes of the input port, and the mode field distribution as following figure.
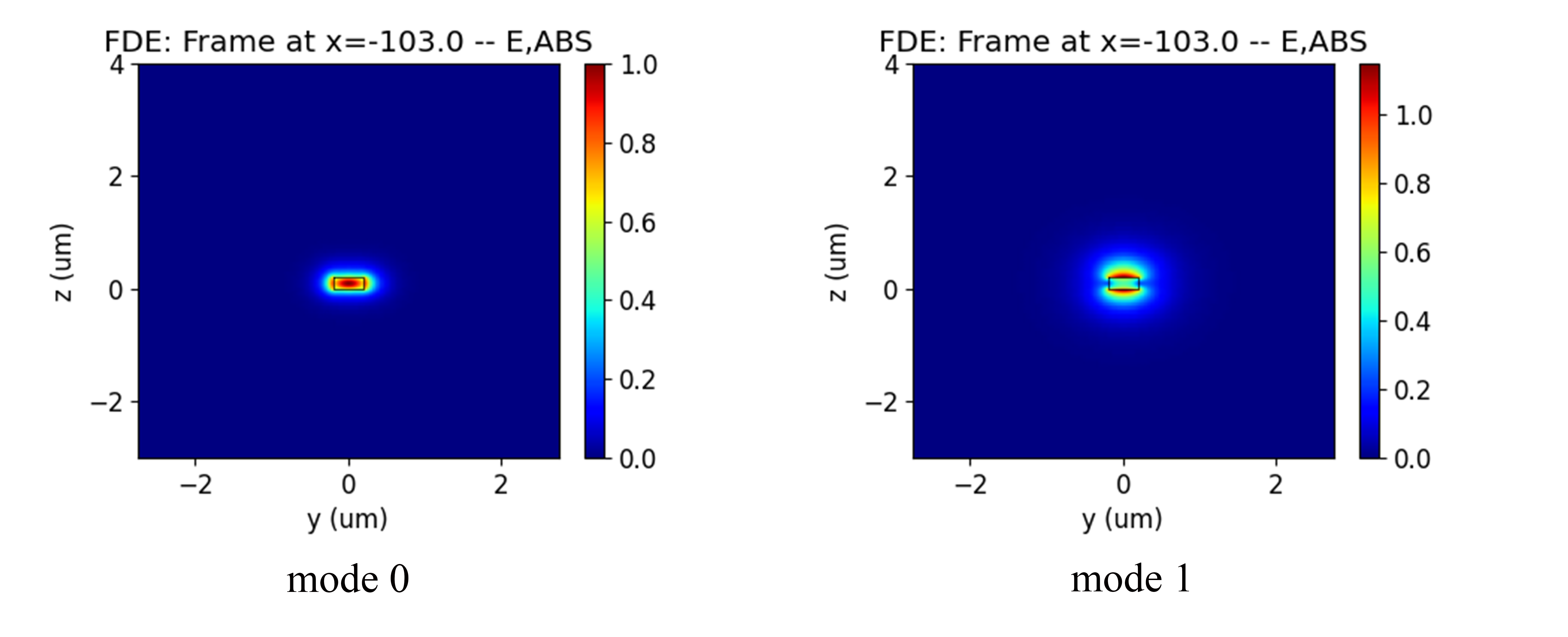
After the propagation calculation is completed, the extracted results can be viewed in the storage path, and the extraction of the results can only be set before the program running. The mode fields of TE polarization at the input and output ends are shown below, it is clearly observed that the output mode field size is larger than the input.
Silicon waveguides have a strong ability to limit the light field, but it can leak into the environment when the waveguide size is too small. By adding a low refractive index waveguide outside the taper waveguide, the leaked light field is limited and the size of the mode spot is increased.
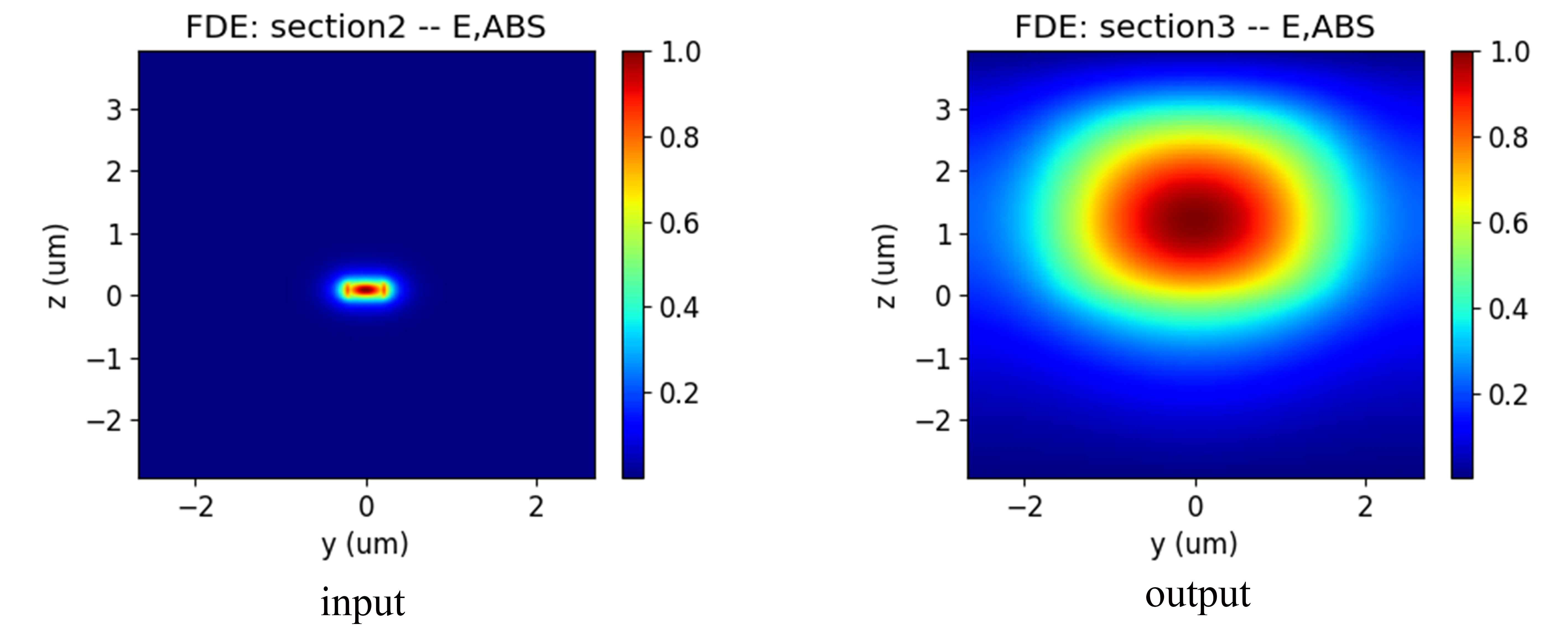
2.2 EME Propagation
The EME solver first calculates the mode of the cell boundary cross-section, and then obtains the scattering matrix for each cross-section by matching the tangential electric and magnetic fields. After bidirectional transmission of the scattering matrix for each cross-section, the S-matrix of the entire device can be obtained. To ensure the accuracy of the calculation results, the number of calculated modes in the cross-section can be gradually increased until the results converge.
After bidirectional transmission calculation of mode, the electric field distribution in the transmission direction can be constructed. The distribution of the electric field is shown in the following figure.
The EME propagation calculation all modes, but only returns the S-matrix of the port mode. As shown in the figure below, the S-matrix is a 2∙2 matrix, where S21 represents the absolute value of the transmission coefficient from port 1 input to port 2 output. Due to the symmetry of the transmission behavior, S12=S21.
Analysis and Discuss
When calculating the area of structural change in EME, it is necessary to divide the structure into multiple cells, and the calculated modes are located at interface between adjacent cells. The more cells divided, the more accurate the characterization of the structure. In the adiabatic tapered waveguide region, the number of cells divided is too small, and the calculated cross-section area varies greatly, resulting in a strong staircase effect. Therefore, before calculating EME, it is necessary to divide the structure into enough cells to ensure the accuracy of the results.
It should be noted that when calculating the EME transmission of taper waveguide, we need to use the "sub_cell" method, which can reduce the non physical reflection caused by the step change of the unit cross-section. Within the range of input and output straight waveguides, the cross-section of the waveguide remains unchanged, and the "none" method is used to calculate the transmission.
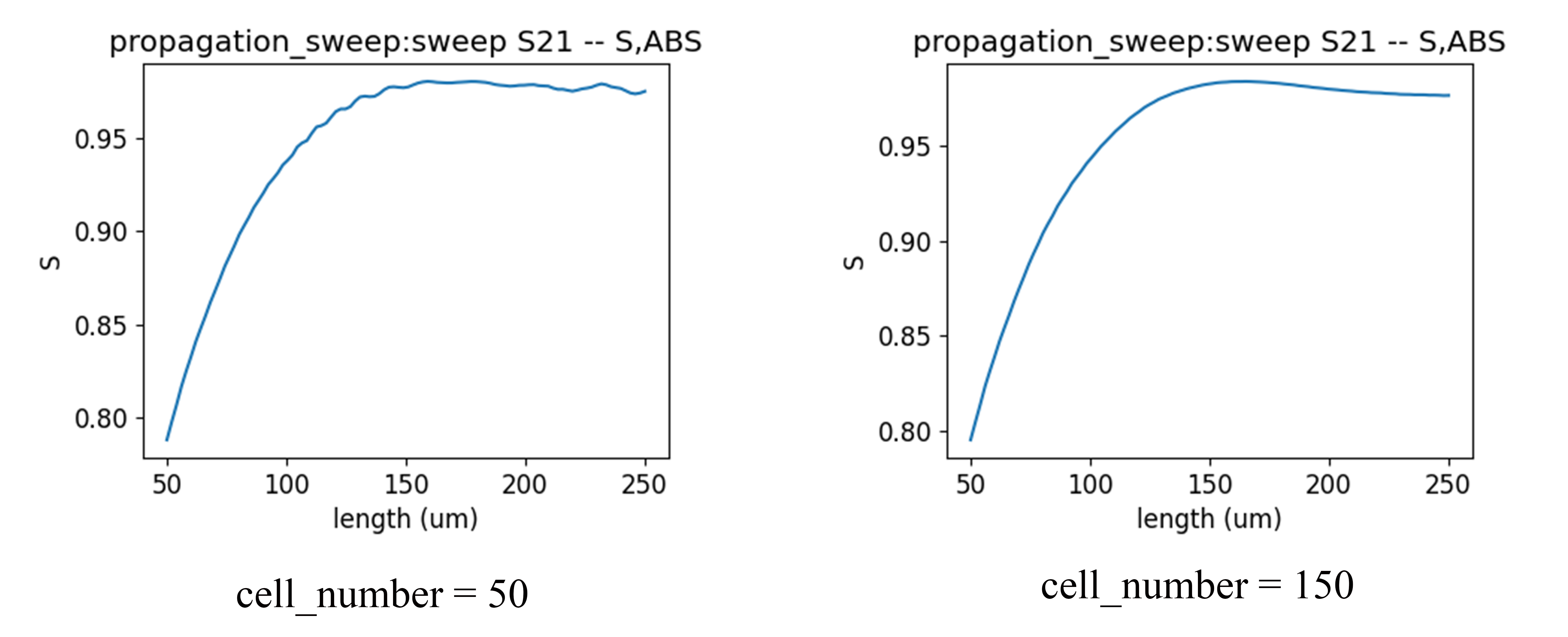
In order to meet the adiabatic condition, we set "run_length_sweep" to True and conducted a length sweep of 50-250 um in the tapered silicon waveguide area. The number of cells divided in the region where the silicon waveguide changes is 50. As shown in the following figure. When the sweeping length is greater than 100 um, the transmission coefficient S21 will fluctuate with the increase of length. When we increase the number of tapered silicon waveguide to 150, the transmission coefficient curve between the sweeping length of 50-250 um becomes smooth. Therefore, in addition to ensuring the number of modes in the unit cross-section, the EME simulation should also have sufficient number of cells.
If you need to sweep the wavelength, you can use "wavelength_sweep" to turn on wavelength sweep. Similar to length sweep, it is necessary to input the starting and ending wavelength and the number of wavelength points in the EME simulation. At each frequency point, the modes of all cell interfaces and EME propagation parts are also calculated. Therefore, wavelength sweep will take longer than length sweep.
References
[1] T. Tsuchizawa et al, “Microphotonics devices based on silicon microfabrication technology”, IEEE J. Select. Topics Quantum Electron. 11, 2005, 232-240